The term matroid is more often connected with mathematics. In mathematics, a matroid is a mathematical structure that abstracts the notion of independence and dependence in a set system.
Matroids have applications in various areas of mathematics, computer science, and beyond.
Matroid theory
Matroid theory is a branch of mathematics that focuses on studying a specific type of combinatorial structure known as a “matroid.”
Definition of a Matroid
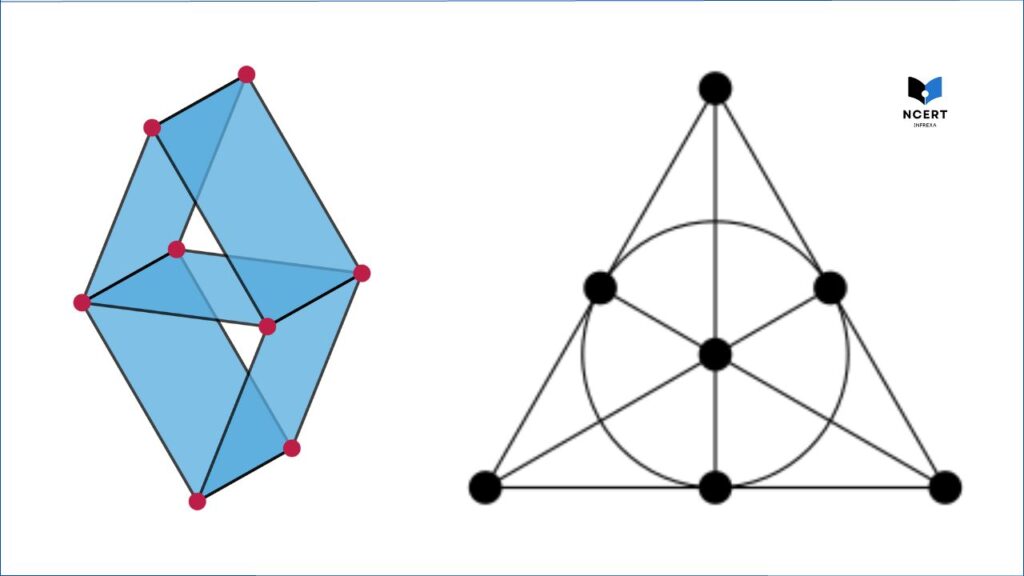
A matroid is a fundamental concept in the field of combinatorics and discrete mathematics that abstracts the concept of independence and dependence within a set system. Formally, a matroid is defined as follows:
A matroid is a pair (E,I), where:
- E is a finite set, often referred to as the “ground set.”
- I is a collection of subsets of E called “independent sets.” These independent sets satisfy three properties:
- The empty set ∅ is in I.
- If X ∈ I and Y ⊆ X, then Y ∈I (hereditary property).
- If X, Y ∈ I and ∣X∣ < ∣Y∣, then there exists an element e ∈ Y ∖ X such that X ∪ {e} ∈ I (exchange property).
The elements of I are the “independent sets,” and they represent subsets of the ground set E that satisfy the independence properties of a matroid. The exchange property is a key defining characteristic of matroids, capturing the idea that if you have two independent sets of different sizes, you can “exchange” an element from the larger set with an element from the smaller set while still maintaining independence.
The concept of matroids provides a unified framework to study various combinatorial structures, such as graphs, vectors, and more, by abstracting their common properties related to independence.
Matroid theory has applications in graph theory, linear algebra, combinatorial optimization, coding theory, and other areas of mathematics and computer science. Here is more:
10 Applications of Metroid in the real world
Matroid theory and its associated concepts have a wide range of applications in real-world scenarios, often providing elegant solutions to complex problems in various fields.
Here are some examples of how matroids and matroid-like structures are applied in practical situations:
1. Graph Theory: Graphs and matroids are closely related. Matroid theory contributes to graph algorithms, network design, and optimization problems. For example, in network design, matroids can help determine the optimal set of edges for spanning trees or minimum spanning trees.
2. Coding Theory: Matroids have applications in coding theory, particularly in designing error-correcting codes. Matroid-based codes can achieve efficient error correction and detection, crucial in digital communication and storage systems.
3. Operations Research and Optimization: Matroid theory is used in various optimization problems, such as the maximum-weight independent set problem and the greedy algorithm for matroids. These algorithms have applications in scheduling, resource allocation, and more.
4. Combinatorial Geometry: Matroids play a role in combinatorial geometry and arrangements. They can help solve problems related to points, lines, and other geometric objects, which have applications in computer graphics and geographic information systems (GIS).
5. Machine Learning and Data Analysis: Matroid-based methods can be applied in machine learning tasks like feature selection and data clustering. They help identify relevant features and reduce dimensionality, improving the efficiency of algorithms.
6. Bioinformatics: Matroid theory is used in computational biology for tasks like phylogenetic tree construction and sequence alignment. Matroid-like structures provide a way to model relationships and hierarchies in biological data.\
7. Electrical Engineering: Matroids are applied in electrical network analysis and circuit design. They assist in solving problems related to connectivity, flow, and electrical circuits.
8. Economics: In economics, matroid theory is used to study problems like resource allocation, market equilibria, and matching algorithms.
9. Logistics and Transportation: Matroids help solve problems in logistics, transportation, and distribution networks, such as finding optimal paths or routes in networks.
10. Game Theory: Matroid concepts can be applied in cooperative game theory, analyzing the distribution of profits among participants in a cooperative game.
These are just a few examples of the many applications of matroid theory across various fields. The versatility and elegance of matroid-based approaches make them valuable tools for solving complex problems in diverse disciplines.